Každý bod elektrického pole má svoji hodnotu potenciálu. Z každého místa je v něm na přenesení náboje Q do místa s nulovým potenciálem třeba vykonat určitou práci W.

V elektrickém poli jsou ale místa, která mají stejný potenciál. Přenášíme-li z těchto míst elektrický náboj do jiného místa, které má nulovým potenciálem, vykonáme vždy stejnou práci.
Místa v elektrickém poli, která mají stejný potenciál, tvoří hladinu potenciálu, tzv. ekvipotenciální plochu.
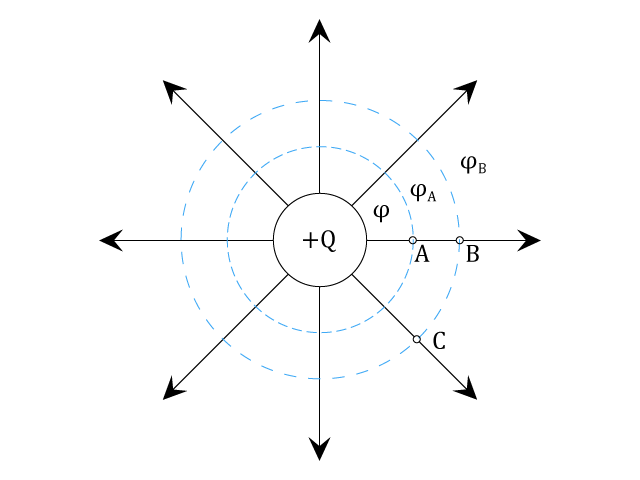
Jestliže se má elektrický náboj pohybovat v elektrickém poli jen působením elektrické síly, musí se přemísťovat mezi dvěma místy s rozdílnými potenciály (stejně jako těleso může padat jen z místa, která má jinou výšku než místo dopadu).

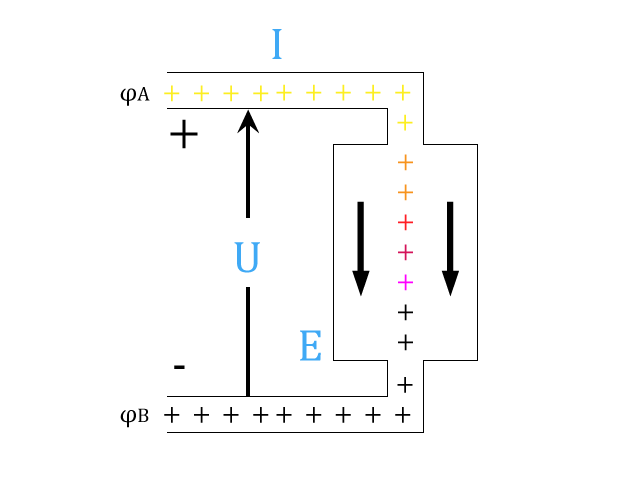
Rozdíl potenciálů mezi dvěma místy v elektrickém poli se nazývá napětí.
$$ U = \varphi_A – \varphi_B $$
Jednotkou elektrického napětí je volt V.
Čím větší je v elektrickém poli rozdíl potenciálů, tím vyšší je napětí a tím větší energie je předána pohybujícímu se náboji.
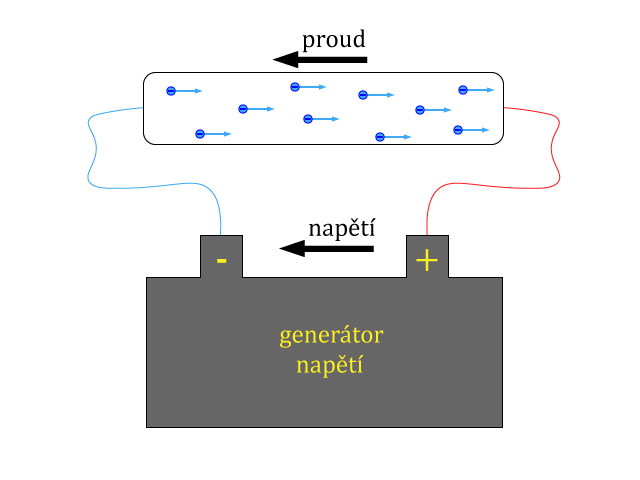
Napětí mezi dvěma místy v elektrickém poli je 1V, jestliže se na přenesení kladného náboje 1C vykoná práce 1J.
$$ U = \frac{W}{Q} $$
Když známe velikost elektrického náboje, který přenášíme a rozdíl potenciálů (napětí), snadno vypočítáme práci potřebnou na přenesení náboje Q mezi dvěma místy elektrického pole
$ W = QU $
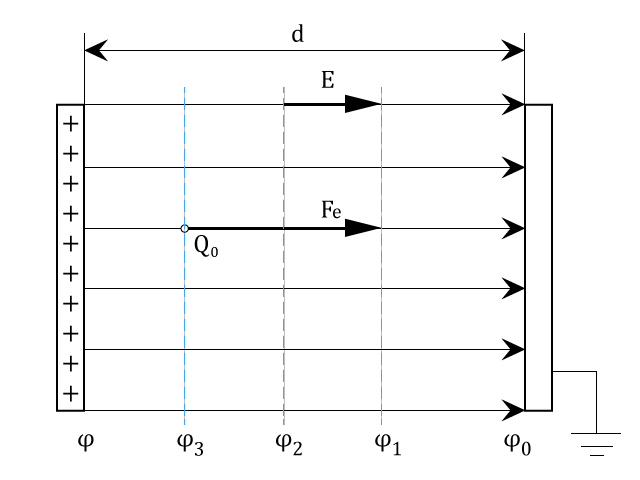
V homogenním elektrickém poli, při pohybu kladného bodového náboje Q z kladné desky na desku s nulovým potenciálem, vykoná elektrické pole práci
$$ W = F_e \cdot I = QEl $$
Potenciál kladné desky: $ φ = El $
Potenciál uzemněné desky $ φ_0 = 0 $
Elektrické napětí mezi oběma deskami: $ U = φ_A – φ_B = El $
Když například elektron proletí potenciálovým rozdílem U, změní se jeho potenciální energie na energii kinetickou (stejně jako u volného pádu tělesa).
$$ eU = \frac{1}{2} mv^2 $$
Můžeme tak vypočítat rychlost elektronu e v elektrickém poli při napětí U, které jej urychlilo.
$$ v = \sqrt{\frac{2eU}{m}} $$
Rychlost a hmotnost elektronů v závislosti na napětí
Urychlující napětí (V) | Rychlost (m/s) | Hmotnost |
100 | $ 5,95 \cdot 10^6 $ | $ 9,12 \cdot 10^{-31} $ |
1 000 | $ 1,87 \cdot 10^7 $ | $ 9,15 \cdot 10^{-31} $ |
10 000 | $ 5,85 \cdot 10^7 $ | $ 9,30 \cdot 10^{-31} $ |
100 000 | $ 1,65 \cdot 10^8 $ | $ 11,0 \cdot 10^{-31} $ |
1 000 000 | $ 2,83 \cdot 10^8 $ | $ 29,2 \cdot 10^{-31} $ |
3 100 000 | $ 2,97 \cdot 10^8 $ | $ 64,6 \cdot 10^{-31} $ |
V homogenním elektrickém poli s intenzitou $ 10^5 V \cdot m^{-1} $ se ve směru siločar pohybuje elektron po dráze 30 cm. Jakou práci vykonaly síly elektrického pole?
Mezi deskami homogenního elektrického pole se pohyboval elektron rychlostí $ 70000 \, km \cdot s^{-1} $. Jaké elektrické napětí je mezi nabitými deskami?